| Девайсы |
| Софт |
| Статьи |
| Контакты |
Упрощенная SPICE-модель контура индукционного нагревателяВ статье описан способ создания упрощенной модели существующего контура индукционного нагревателя. Контур заменен эквивалентной схемой, состоящей из согласующего трансформатора, конденсатора, эквивалентных R и L элементов, величины которых определены по затухающим колебаниям, вызванным генератором ударного возбуждения. Измерения производятся при помещении разных объектов в индуктор после чего формируются наборы измеренных эквивалентных параметров для каждого объекта. Полученные параметры заносятся в LTSpice-модель. В итоговой модели не предполагается учет динамики изменения параметров в процессе нагрева объектов. Исходные данные
При построении модели описанным способом будут использованы не все данные, здесь они приведены для общего представления. Эквивалентная схема
Эквивалентная схема содержит следующие элементы: Rprim – сопротивление постоянному току первичной обмотки (исходные данные); Lprim – индуктивность первичной обмотки (исходные данные); Lsec – индуктивность вторичной обмотки (расчет); C – контурный конденсатор (исходные данные); Requ – эквивалентное сопротивление контура (измерения); Lequ – эквивалентная индуктивность контура (измерения). Для определения индуктивности вторичной обмотки (витка) воспользуемся измеренной величиной индуктивности первичной обмотки и соотношением витков: 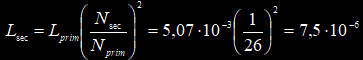 Гн Гн
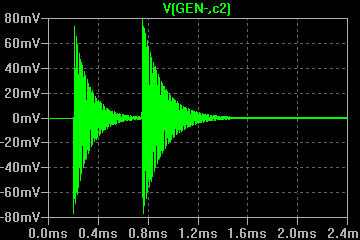
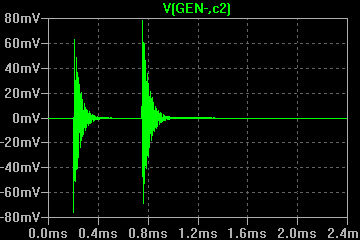
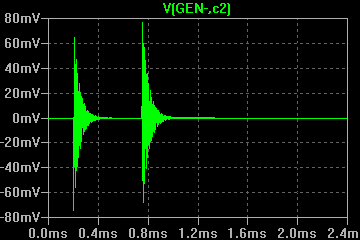
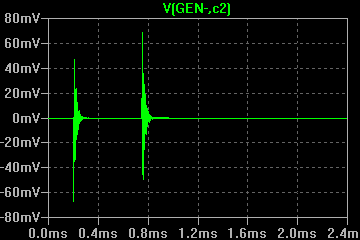
С применением генератора ударного возбуждения снимаются осциллограммы затухающих колебаний при помещении в индуктор различных объектов. Параметры осциллограмм заносятся в таблицу 2, к ним относятся: F0 - частота свободных колебаний; VA - амплитуда первого или второго колебания; VB - амплитуда колебания, следующего за предыдущим измеренным (VA). По измеренным параметрам рассчитываются промежуточные (Q - добротность) и недостающие для модели параметры (Lequ, Requ): 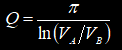 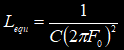 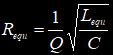
В результате сравнения модели и эксперимента видно сходство осциллограмм, поэтому принимаем полученные эквивалентные параметы контура для применения в последующих моделях. Далее производится эксперимент с генератором ударного возбуждения, подключенным уже к первичной обмотке трансформатора, как изображено в модели на рисунке 7.
На рисунке 8 изображены осциллограммы напряжения на контурном конденсаторе в эксперименте и в модели. Видно различие скорости затухания. К тому же кривая затухания колебаний в эксперименте не описывается экспонентой (переменный коэффициент затухания), что может быть следствием того, что эквивалентное активное сопротивление в системе, влияющее на скорость затухания, зависит от амплитуды колебаний.
Различия осциллограмм колебаний, проявившиеся в присутствии согласующего трансформатора, могут говорить о том, что в модели трансформатора не всё учтено. Подробно методика моделирования трансформатора описана в [1]. В следующей модели добавлена нелинейная индуктивность L4, которая учитывает гистерезисные свойства феррита (Hc - коэрцитивная сила, А*вит/м; Bs - индукция насыщения, Тл; Br - остаточная индукция, Тл), а также площадь поперечного сечения A, длину средней линии Lm и число витков первичной обмотки N. Параметры ферритов можно посмотреть в [2]. Трансформатор намотан на ферритовом сердечнике из 3-х колец М2000НМ1 45х28х12, тогда: 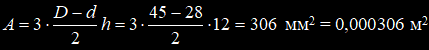 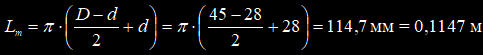
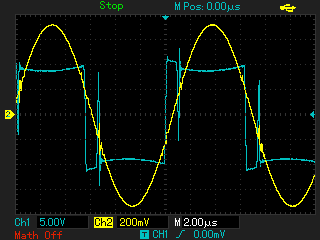
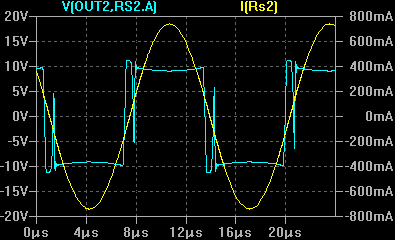
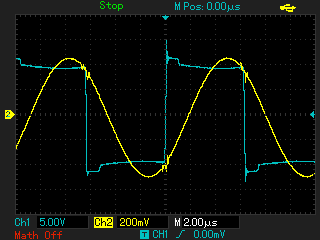
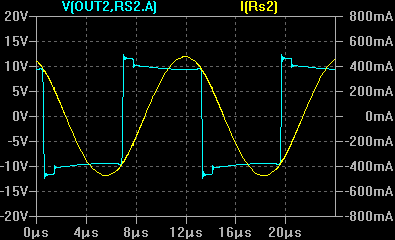
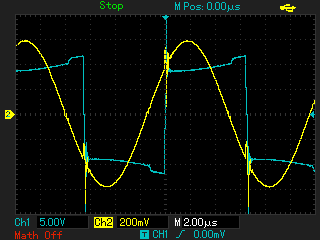
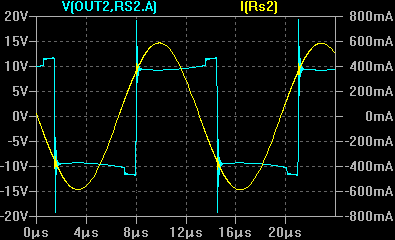
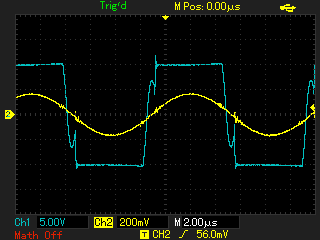
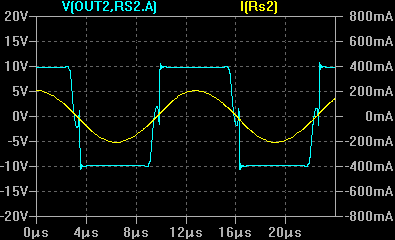
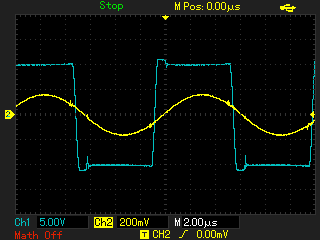
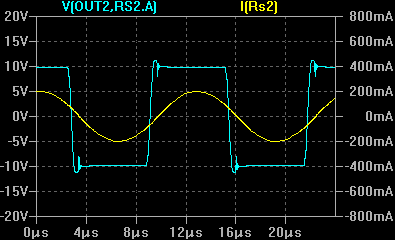
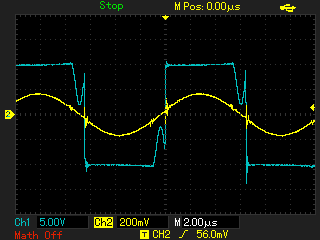
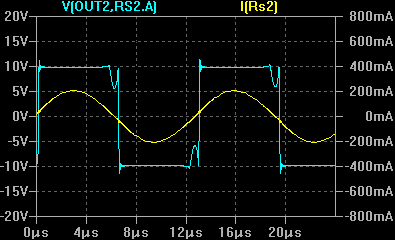
В последнем случае осциллограммы имеют лучшее сходство, поэтому в качестве модели контура решено оставить вариант, изображенный на рисунке 9. Далее производятся эксперименты с подключением испытуемого контура к макету мостового инвертора. Инвертор будет управляться генератором, с регулируемой частотой. Будут производиться сравнения осциллограмм напряжения и тока на выходе инвертора при помещении в индуктор объектов, под которые была ранее рассчитана модель.
Из сравнения осциллограмм модели и эксперимента в целом видно сходство как по амплитудам, так и по форме. Поэтому полученная модель контура может быть применена для моделирования некоторых режимов работы установки.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  © WhiteArc.RU, 2011-2025 © WhiteArc.RU, 2011-2025 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Рисунок 1 - Вид контура индукционного нагревателя
Рисунок 1 - Вид контура индукционного нагревателя
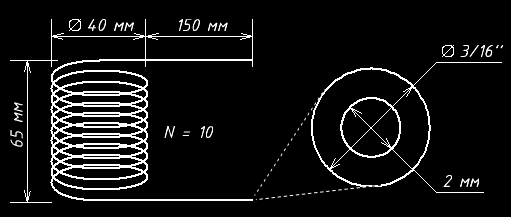 Рисунок 2 - Геометрия индуктора
Рисунок 2 - Геометрия индуктора
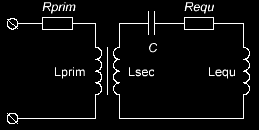 Рисунок 3 - Эквивалентная схема контура
Рисунок 3 - Эквивалентная схема контура
 Рисунок 4 - Схема экспериментальной установки
Рисунок 4 - Схема экспериментальной установки
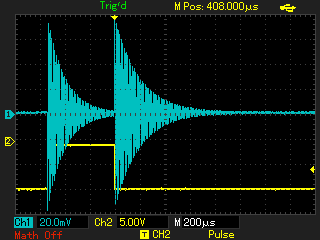
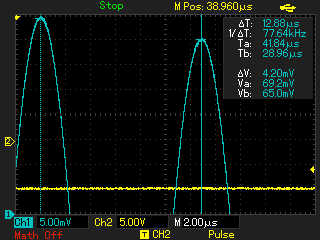 Рисунок 5 - Осциллограмма свободных колебаний с пустым индуктором (пример)
Рисунок 5 - Осциллограмма свободных колебаний с пустым индуктором (пример)
 Рисунок 6 - Модель для сверки с экспериментом (
Рисунок 6 - Модель для сверки с экспериментом ( Воздух
Воздух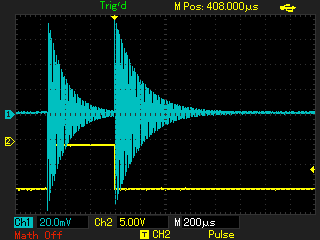
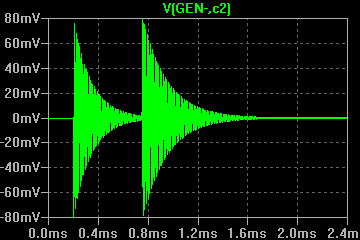
 Латунь
Латунь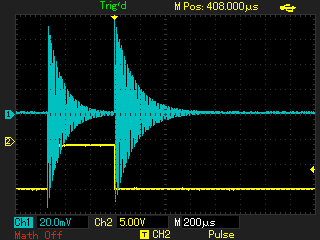
 Болт М10
Болт М10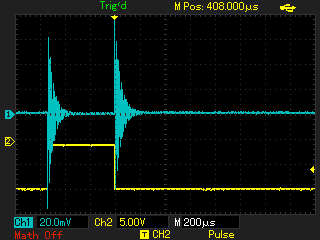
 Болт М14
Болт М14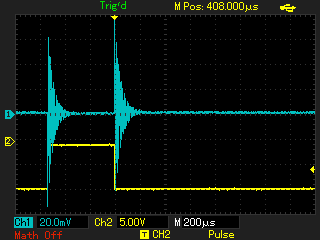
 Тигель
Тигель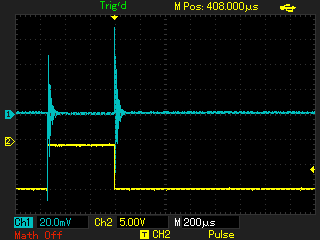
 Тигель + болт М10
Тигель + болт М10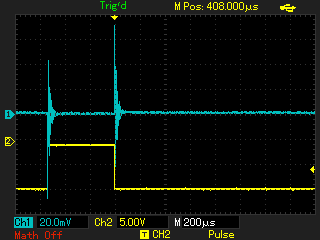
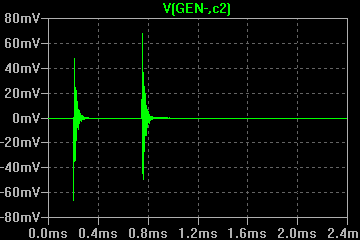
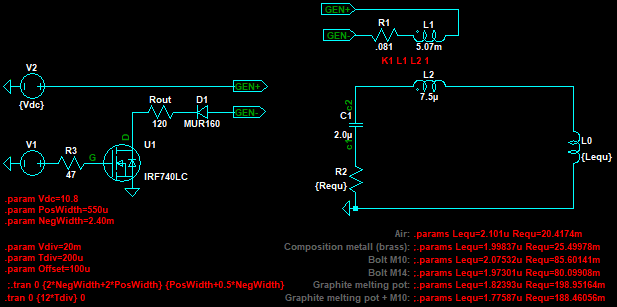 Рисунок 7 - Модель с подачей импульса на первичную обмотку трансформатора (
Рисунок 7 - Модель с подачей импульса на первичную обмотку трансформатора (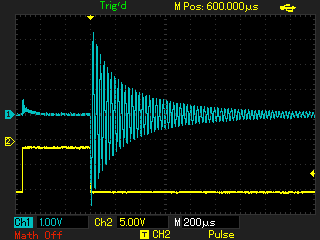
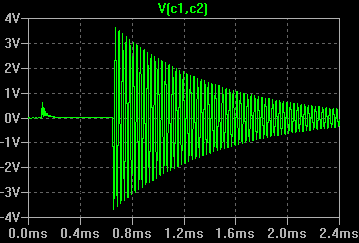 Рисунок 8 - Осциллограмма напряжения на C1 при подаче импульса на первичную обмотку трансформатора
Рисунок 8 - Осциллограмма напряжения на C1 при подаче импульса на первичную обмотку трансформатора
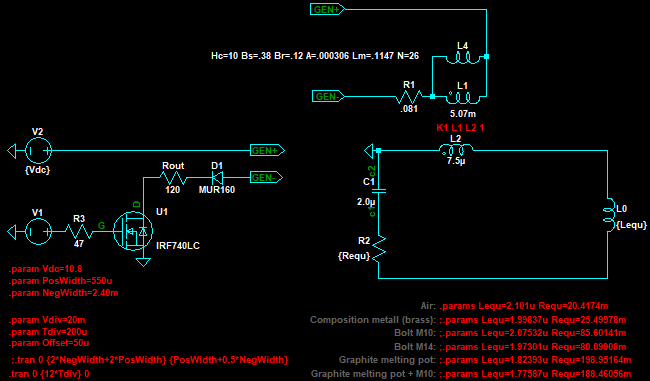 Рисунок 9 - Модель с добавлением нелинейной индуктивности трансформатора (
Рисунок 9 - Модель с добавлением нелинейной индуктивности трансформатора (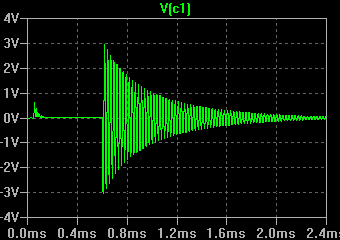 Рисунок 10 - Осциллограмма напряжения на C1 при подаче импульса на первичную обмотку трансформатора
Рисунок 10 - Осциллограмма напряжения на C1 при подаче импульса на первичную обмотку трансформатора
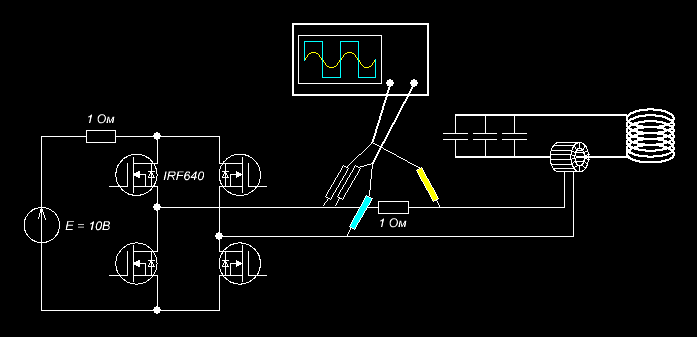 Рисунок 11 - Модель с подачей импульса на первичную обмотку трансформатора
Рисунок 11 - Модель с подачей импульса на первичную обмотку трансформатора
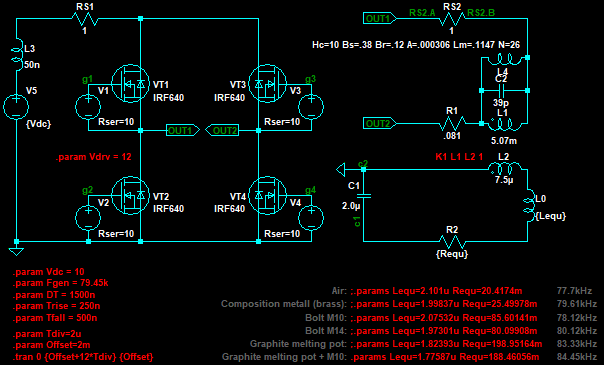 Рисунок 12 - Модель с подачей импульса на первичную обмотку трансформатора (
Рисунок 12 - Модель с подачей импульса на первичную обмотку трансформатора (