Определение частоты и добротности LC-контура с помощью генератора ударного возбуждения
Описанные в статье способы определения частоты и добротности контура основаны на анализе осциллограмм затухающих колебаний,
возникающих в LC-контуре после отключения внешнего источника, передавшего контуру энергию перед отключением.
Эти колебания (собственные или резонансные) с течением времени затухают и по скорости их затухания
определяется добротность контура, а по периоду колебаний - резонансная частота контура.
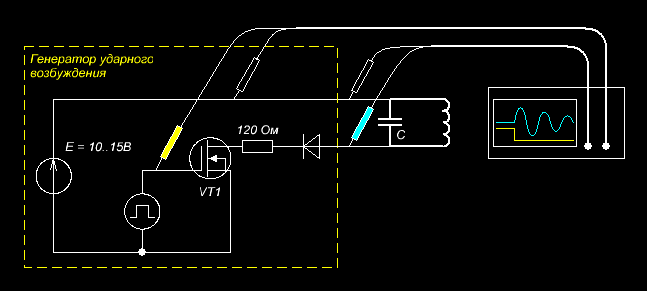 Рисунок 1 - Схема экспериментального макета
Рисунок 1 - Схема экспериментального макета
Генератор
Источником, передающим энергию контуру в данном случае служит генератор ударного возбуждения.
Генератор подключается к испытуемому параллельному LC-контуру и подает на него импульсы тока.
Длительность одиночного импульса генератора много больше периода собственных колебаний контура,
поэтому перед спадом импульса ток в индукторе успевает установиться и достичь максимума, а на контурном конденсаторе при этом напряжение равно падению напряжения на активном сопротивлении индуктора (далее считаем нулевым).
К моменту окончания импульса в индукторе запасается энергия, пропорциональная индуктивности и квадрату протекающего на данный момент тока (ограниченного прежде всего сопротивлением R1).
Далее импульс прерывается со скоростью dI/dt (≈500нс), что приводит к возникновению в индукторе ЭДС самоиндукции,
которая начинает заряжать конденсатор контура. После передачи всей энергии индуктора в кондерсатор, ток заряда прекращается и
конденсатор уже начинает "разряжаться" на индуктор и электрическая энергия снова перетекает в индуктор. По пути часть энергии уходит на
нагрев активного сопротивления и на излучение электромагнитных волн, поэтому с каждым новым колебанием
амплитуда тока и напряжения снижается.
 Рисунок 2 - Схема генератора ударного возбуждения
Рисунок 2 - Схема генератора ударного возбуждения
Генератор на базе таймера NE555 (КР1006ВИ1) собран в виде макета. Резистором RP1 регулируется длительность импульса в пределах 0-7,5 мс.
Резистором RP2 регулируется период 8,3-18 мс, что соответвтвует 55-120 Гц. Ключом служит транзистор VT1, рассчитанный на 400В 10А.
Резистор R1 ограничивает выходной ток до 100 мА при напряжении питания 12В, чего хватает для поставленных задач.
Диод VD1 препятствует прохождению тока обратной полярности через внутренний диод сток-исток транзистора VT1 при колебаниях в испытуемом LC-контуре после закрытия VT1.
С учетом того, что к выходу генератора могут подключаться нагрузки с индуктивной составляющей, а прерывание импульса происходит достаточно быстро,
то транзистор и диод VD1 должны быть рассчитаны на обратное напряжение в несколько сотен вольт.
Снабберы в данном случае не применяются намеренно, поскольку они внесут искажения в эксперименты.
 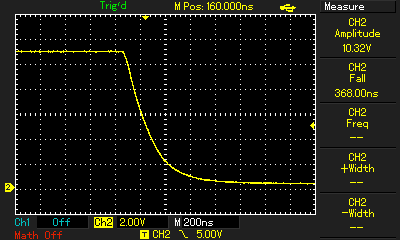 Рисунок 3 - Осциллограммы напряжения на затворе VT1 на настроенном генераторе
Рисунок 3 - Осциллограммы напряжения на затворе VT1 на настроенном генераторе
Испытуемый контур
В качестве испытуемого используется параллельный LC-контур, у которого необходимо определить резонансную частоту
и добротность. Контур состоит из индуктора без сердечника, намотанного на бумажной трубке.
Контурный конденсатор, емкостью C=100нФ установлен параллельно подключенному индуктору на одной макетной плате с генератором.
 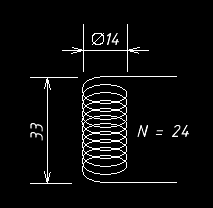 Рисунок 4 - Фото экспериментального макета
Рисунок 4 - Фото экспериментального макета
Перед измерениями рассчитаем индуктивность индуктора и частоту контура (необязательно), чтобы потом сравнить с измеренной величиной частоты:
Измерение частоты
На макете, собранном по схеме (рис. 1) снимем осциллограмму собственных колебаний контура.
Если осциллограф имеет более одного луча, то одиним лучом можно выводить управляющий сигнал с затвора генератора
и по нему же синхронизироваться, настроив триггер по спаду этого сигнала.
А вторым лучом выводить напряжение на конденсаторе контура, которое покажет собственные колебания контура.
Так как в осциллографе общие (минусовые) концы щупов не развязаны, то подключить одновременно один к минусу,
а второй к стоку или к +Vdc нельзя, будет практически КЗ. Поэтому минусовые выводы обоих щупов подключаем к +Vdc (рис. 1).
Луч управляющего сигнала окажется смещен вниз на величину Vdc. Триггер также нужно перенастроить с учетом смещения сигнала.
Синхронизироваться можно не используя сигнал с генератора, настроив триггер по пику первого колебания. Но, тогда при изменении
параметров контура, амплитуда колебаний будет меняться и синхронизация будет каждый раз сбиваться.
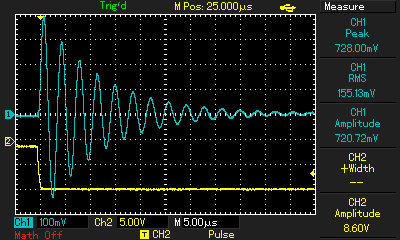  Рисунок 5 - Осциллограмма собственных колебаний контура
Рисунок 5 - Осциллограмма собственных колебаний контура
По периоду между пиками колебаний (вторая осциллограмма рис. 5) определяем собственную частоту колебаний контура.
Хотя, на второй осциллограмме пики отмечены вручную, а период и частота уже измерены осциллографом, ниже показаны вычисления вручную.
Период T=3,6клетки*1,0мкс=3,6мкс.
В формулу расчета частоты подставляем уточненное по осциллографу значение периода 3,56мкс, тогда частота F и погрешность расчета δF составит:
Измерение добротности
По осциллограмме затухающих колебаний добротность можно определить несколькими способами:
- По числу колебаний, за которое амплитуда снижается в e раз (при низкой добротности точность невысока);
- По логарифмическому декременту затухания λ, рассчитанному по амплитудам двух колебаний, идущих одно за другим;
- По коэффициенту затухания β, подобранному при аппроксимации огибающей затухания.
Способ 1
На осциллограмме рис.6 максимальная амплитуда колебания составляет 400мВ, тогда нижний предел, до которого нужно считать колебания, будет на уровне 400/e≈400/2,72≈147мВ.
Этот предел отмечаем на графике осцилляций (красной линией) и считаем число периодов с амплитудами колебаний выше этого предела,
по графику это Ne=3. Тогда добротность будет приблизительно равна:
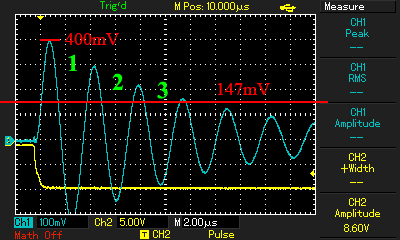 Рисунок 6 - Осциллограмма затухающих колебаний
Рисунок 6 - Осциллограмма затухающих колебаний
Способ 2
На осциллограмме затухающих колебаний определяем амплитуды двух первых колебаний (необязательно первых), идущих одно за другим.
На рисунке 5 они отмечены (Va=400mV, Vb=284mV).
Рассчитаем логарифмический декремент затухания λ и добротность Q:
Способ 3
Для вычисления добротности нужно найти коэффициент затухания β.
Зная, что огибающая затухающих колебаний описывается экспоненциальным законом (рис. 7), можно подобрать
искомый коэффициент затухания, с которым уравнение станет наиболее точно описывать экспериментальную кривую.
Это можно делать в Excel, MathCad и другими средствами. Если делать это в Excel, то нужно подбирать коэффициенты,
пока расхождения между искомым и расчетным графиками не станут минимальными.
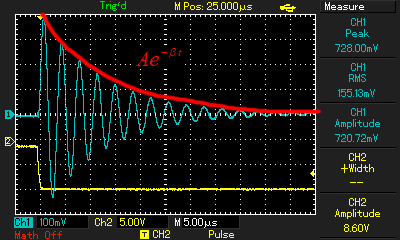 Рисунок 7 - Экспоненциальный закон затухания
Рисунок 7 - Экспоненциальный закон затухания
Ниже приводится пример аппроксимации в MathCad.
Для этого зафиксируем точки огибающей затухания в таблицу, в MathCad'е формируем два вектора X и Y и передаём функции expfit().
Результатом является вектор Z с найденными коэффициентами экспоненциальной функции f(t)=Aeβt+C.
Время в таблице фиксируется относительно начала колебаний, а напряжение относительно нуля. Хотя значения напряжения могут быть занесены со смещением, тогда будет найдена функция со смещением C, что не повлияет на искомый β.
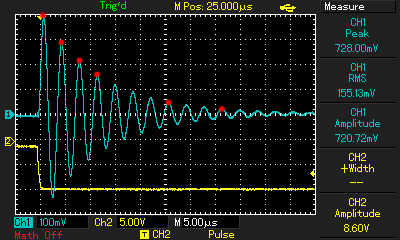 Рисунок 8 - Точки кривой затухания
Рисунок 8 - Точки кривой затухания
| Время, с | Напряжение, В |
|---|
| 0,000001 | 0,4 |
| 0,000004 | 0,284 |
| 0,000008 | 0,22 |
| 0,000011 | 0,16 |
| 0,000026 | 0,05 |
| 0,000036 | 0,02 |
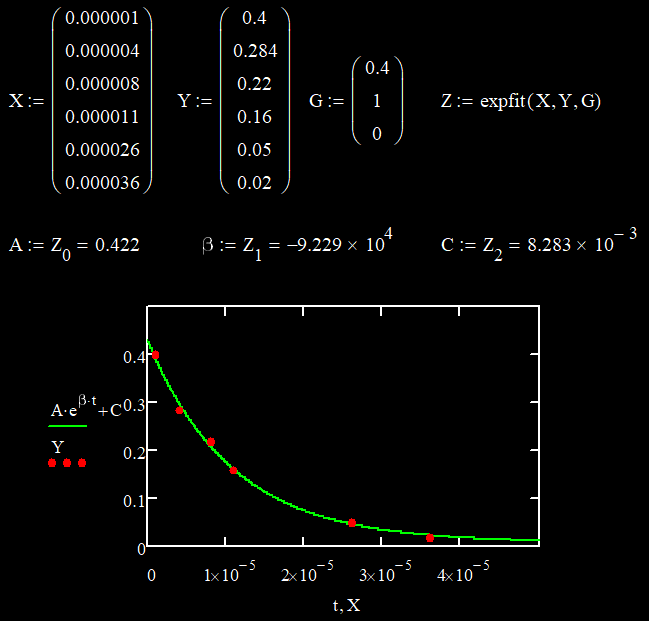 Рисунок 9 - Аппроксимация по экспериментальным данным
Рисунок 9 - Аппроксимация по экспериментальным данным
В результате аппороксимации получены коэффициенты функции, которая рисует график максимально близкий к заданным точкам (рис. 7).
Получен коэффициент затухания |β|=92290, с учетом которого определим добротность контура:
Выводы:
Точность определения добротности всеми способами ограничивается точностью измерения исходных параметров. Так для 1-го способа подходят
случаи с относительно высокой добротностью, когда учитывается большое число целых периодов Ne.
Способ 2 удобен для случаев с относительно низкой добротностью, когда различима разность амплитуд между двумя полуволнами,
чтобы измерить их с достаточной точностью.
Комментарии
|



